自然言語の相関次元は、大規模言語モデルによって生成された高次元ベクトル列にGrassberger-Procacciaアルゴリズムを適用することで測定されます。この方法は、以前はユークリッド空間でのみ研究されていましたが、本研究では、統計多様体上にFisher-Rao距離を用いて再定式化しました。相関次元は、普遍的に約6.5であることがわかりました。この値は単純な離散ランダム列のそれよりも小さく、Barabási-Albert過程のそれよりも大きいです。 参考文献
音楽
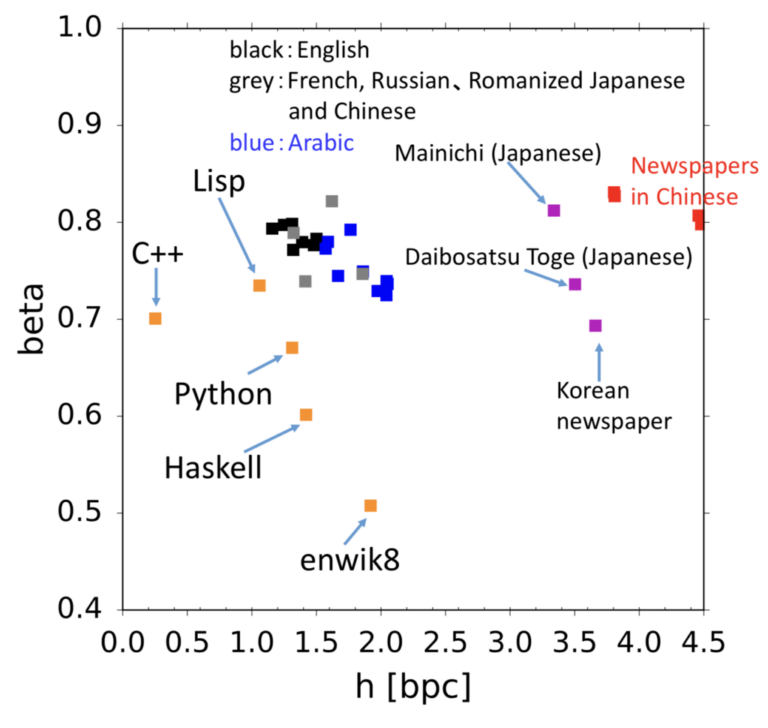
言語、音楽、プログラムなど記号に基づく時系列のエントロピーレートを算出し、 人の記号の時系列に内在する複雑さを探求しています。長さnの時系列の場合の数を、パラメータhを用いて2hnとして考えてみます。まずランダムなビット列の場合はh=1です。では英語を仮に27文字と考えたとしてその数は27n、にはなりません。なぜなら自然言語の場合、qの後にはuしか続かないなど言語的な制約がさまざまにあるからです。情報理論の父シャノンはh=1.3と算出していますが、hの推定は難しい問題で、自然言語のhが正なのかすら未だにわかっていません。研究室では自然言語に加え、音楽・プログラム・金融データなどさまざまな記号時系列の複雑さを推定する研究を行っています。 参考文献
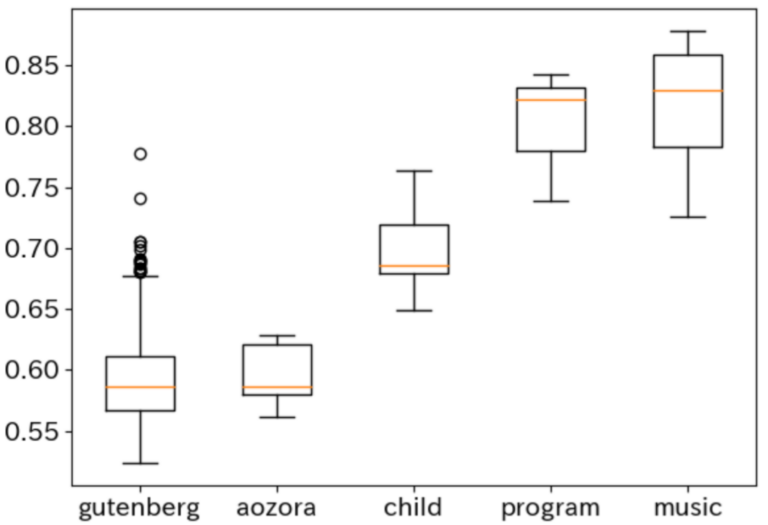
大人に比べて子供の話し言葉はどの程度構造的に複雑なのでしょうか? また、歴史に残る名作は、Wikipediaに比べてどうでしょうか? 言語の構造的複雑さの考察については、文法に対する『チョムスキー階層』が知られ、 書き換えルールの制約によって言語が階層的に捉えられます。 研究室ではこれとは別に、文書に内在するスケーリング則から得られる統計量を利用し、 構造の複雑さを計量する方法を探求しています。 参考文献
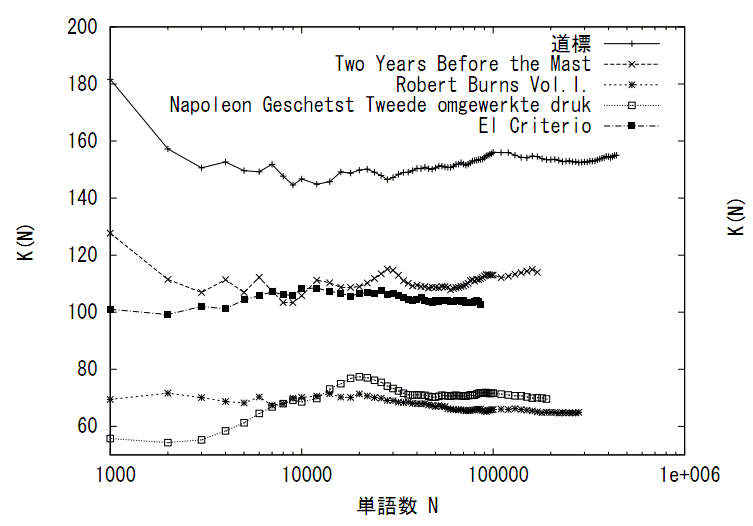
様々な種類のデータに対して様々な統計量が数理的に考察されてきました。自然言語のテキストに対しては著者や言語種、ジャンルなど、その種類を量的に峻別する統計量とは何かが考えられてきました。例えば統計学者Yuleが提案したKがその一つで、これはRenyiの2次エントロピーと等価です。YuleのKはデータ量に依存しない統計量となっており、データの性質を安定的に表す統計量となっています。研究室では、データのスケーリング則との関連をふまえ、このような統計量として何があるかを探究しています。 参考文献