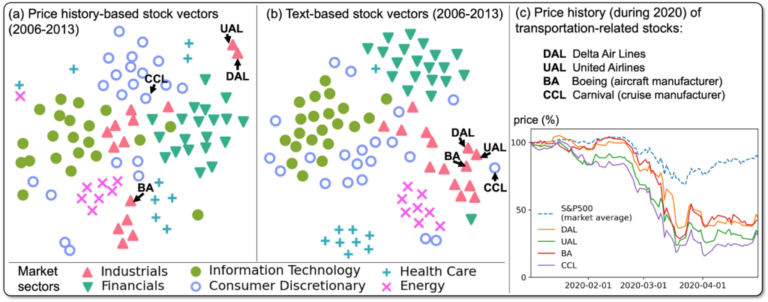
物理経済の理論下では、価格のスケーリング則が知られ、それは市場がなぜ簡単に破綻するのか、 その理由を説明するものです。金融市場の大きな問題の一つは、稀少な事象に起因するリスクの特徴を、 いかに捉えるか、という点にあります。たとえば、コロナ禍は稀少な事象例で、その際の株価の動向は、 過去のデータからモデル化することは難しいのです。この点、新聞などの文書では、 稀な事象を、より強調して記述するものです。このため、価格に加え文書を利用することは、リスクを捉える一つの手段となります。 研究室では、文書データを用いて、経済リスクを計量し応用する方法を研究しています。 参考文献
言語
複雑系の本質的な一面として、イベントが「塊として現れる性質」があります。たとえば、下図は、ある特定の単語群が時系列の中で現れる位置を示しており、上段ほど「稀」な単語に絞って表示しています。最上段を見ると、稀なイベントが塊として現れていることがわかります。統計物理学では、このような性質をゆらぎ解析や長相関として捉える方法論が研究されてきましたが、それは主として数値時系列に対する解析手法となっており、非数値的な時系列での計測方法は確立したとはいえません。研究室では、既存手法を改良し、安定してこのようなゆらぎを計測する方法を模索しています。得られた方法を利用し、系の複雑さを計量することも試みています。 参考文献
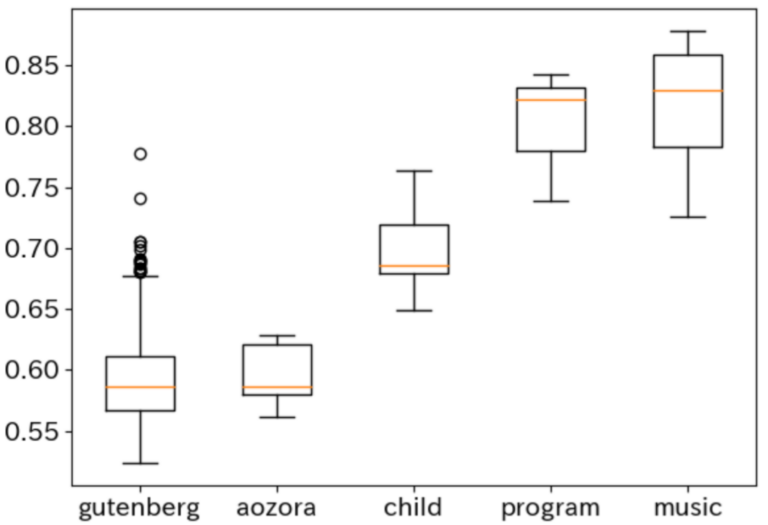
大人に比べて子供の話し言葉はどの程度構造的に複雑なのでしょうか? また、歴史に残る名作は、Wikipediaに比べてどうでしょうか? 言語の構造的複雑さの考察については、文法に対する『チョムスキー階層』が知られ、 書き換えルールの制約によって言語が階層的に捉えられます。 研究室ではこれとは別に、文書に内在するスケーリング則から得られる統計量を利用し、 構造の複雑さを計量する方法を探求しています。 参考文献
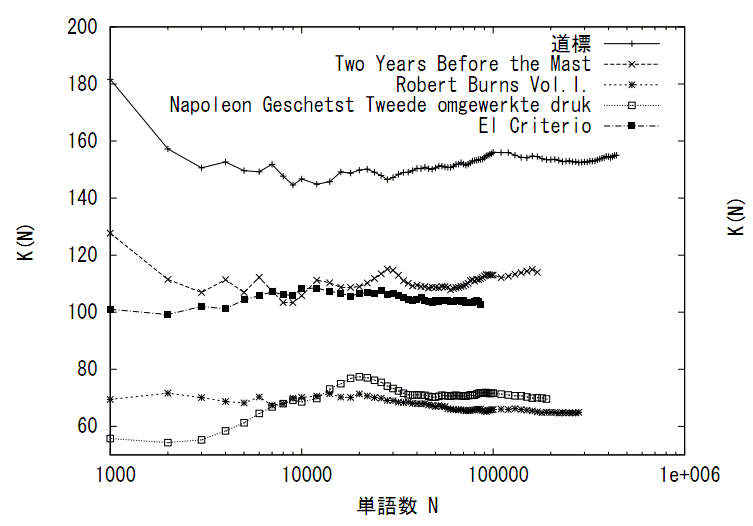
様々な種類のデータに対して様々な統計量が数理的に考察されてきました。自然言語のテキストに対しては著者や言語種、ジャンルなど、その種類を量的に峻別する統計量とは何かが考えられてきました。例えば統計学者Yuleが提案したKがその一つで、これはRenyiの2次エントロピーと等価です。YuleのKはデータ量に依存しない統計量となっており、データの性質を安定的に表す統計量となっています。研究室では、データのスケーリング則との関連をふまえ、このような統計量として何があるかを探究しています。 参考文献
「_月_日_時より_スタート!」「regard _ as _」など、穴空きの定型表現は文書には頻出し、特にツイートやブログでは多用されています。穴空きの定型表現は文法導出に相当し、難しい問題の一つです。研究室では、穴空きの定型表現を最小オートマトンを作成して抽出することを試みています。最小オートマトンは、できる限り重複を重ね合わせた構造を作ります。重複した部分は定型部分、そうでない部分は穴部分として捉えることによって穴空きの定型表現を得ます。基礎的な検証を経て、深層学習で実装し、SNSからのパターン抽出など応用を考えています。 参考文献
生成モデルは、工学上の一つ重要なテーマで、ある系のサンプルを、擬似的に実現する方式のことです。生成モデルを探求することは、系の本質を捉え、それを実現する学習器の能力を吟味し、その構成を再考することにつながります。研究室では、マルコフモデル、文法的モデル、Simon生成過程など既存のモデルに加え、複雑系ネットワーク上のランダムウォーク、AutoencoderやAdversarialなど深層学習生成モデルも含め、複雑系を包括的に再現する試みを行っています。 参考文献
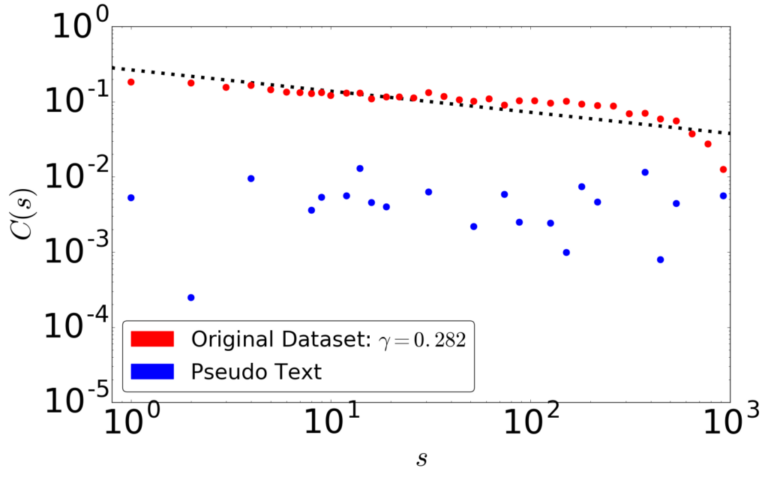
深層学習はデータのどのような側面を捉え、または捉えきれないのでしょうか。 複雑系としての記号の系にはさまざまな経験則が成り立つことが知られています。 研究室では、深層学習が生成する擬似データにどの程度の冪乗則が成り立っているか検証し、 従来の観点からは異なる観点から深層学習を吟味し、深層学習の改良につなげることを考えています。 たとえば右図は、文書は成り立つ長相関が文字レベル深層言語モデルでは成立しないことを示しています。 このような議論は自然言語以外の系、例えば金融市場にも適用することができます。 参考文献
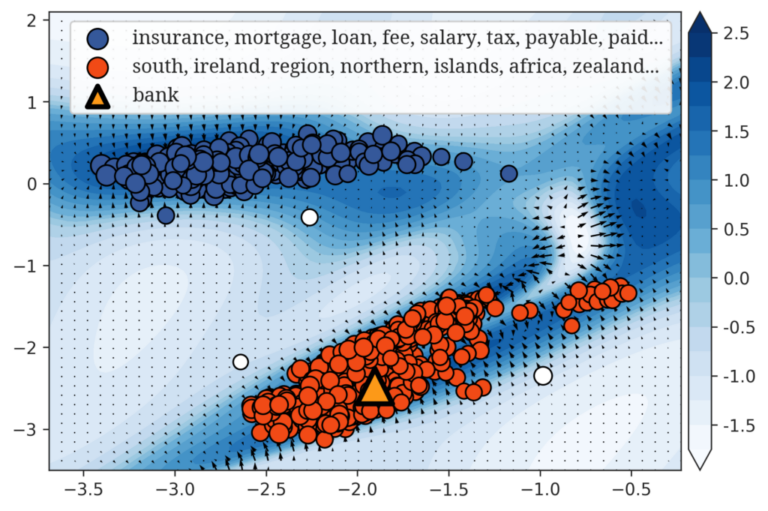
機械学習では単語など文書の要素をベクトルとして表現しなければならず、それを埋め込み表現といいます。 現在の埋め込み表現は、線形ベクトル空間の中に単語をベクトルとして表現しますが、線形空間では、 多義性など単語の持つ非線形な特性を表現することができません。 このため、既存のベクトル表現に代わる数理的な表現を研究しています。 試みとして、FIRE という関数に基づく表現を構築しました。FIREはBERTと同等の性能を有し、単語の意味の数の推定することにおいては、BERTよりも優れている埋め込み表現です。 参考文献