大規模言語モデル(LLM)は自然言語生成において顕著な進歩を遂げている一方で、パープレキシティが低い場合であっても、反復や文のちぐはぐさといった不可解な挙動を依然として示す。このことは、局所的な予測精度を重視するあまり長距離の構造的複雑さを見落としてしまうという、従来の評価指標の本質的な限界を浮き彫りにしている。本研究では、自己相似性を測るフラクタル幾何学的な尺度である「相関次元」を導入し、言語モデルの観点から知覚されるテキストの認識論的複雑さを定量化する。この指標は、言語の階層的な再帰構造を捉えることで、局所的および大域的な性質を統一的な枠組みのもとで橋渡しする役割を果たす。大規模な実験を通じて、相関次元が (1) 事前学習過程における3つの異なるフェーズを明らかにし、(2) 文脈依存的な複雑さを反映し、(3) モデルのハルシネーション傾向を示唆し、さらに (4) 生成テキストに現れる複数のデジェネレーション形態を高い信頼性で検出できることを示す。我々の手法は計算効率に優れ、4ビット精度までのモデル量子化に対しても頑健であり、Transformer や Mamba をはじめとする広範な自回帰アーキテクチャに適用可能である。また、LLM の生成ダイナミクスに対して新たな洞察を提供する。 参考文献 Du, X., & Tanaka-Ishii, K….
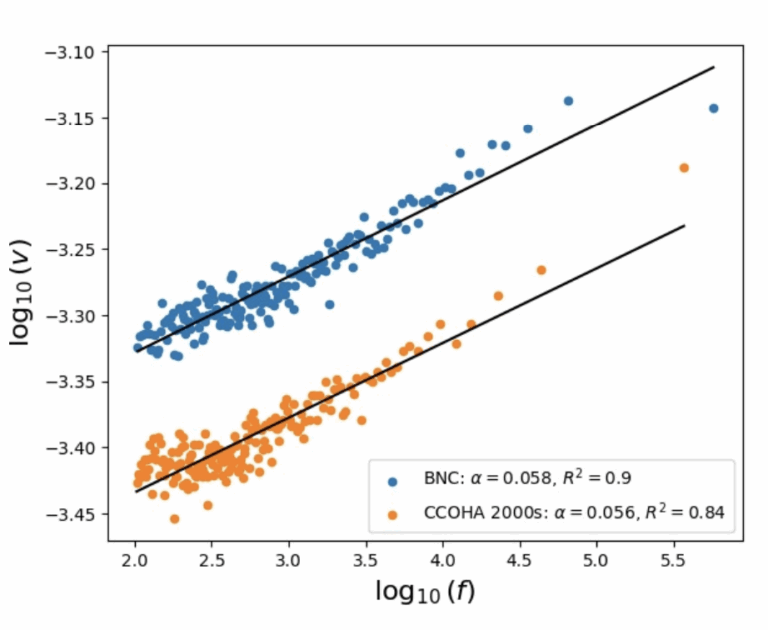
語の出現頻度と語義数のあいだには冪乗則が成り立つことをZipfが報告しており、「Zipf の意味頻度則」として知られます。これはいわゆるZipf則とは別の法則です。従来、語義数は辞書中の意味の数で計測されていましたが、すると、辞書に登録のない単語について、意味頻度則を調べることができません。本研究では、言語モデル(LM)から得られる単語ベクトルのばらつきを計測し、それと頻度の間に冪乗則が成り立つことを示しました。この冪乗則は、ある程度大きな言語モデルでないと観測されないことも報告しています。甲南大学・永田亮先生と共同研究の成果です。 参考文献 Nagata, R., & Tanaka-Ishii, K. (2025, July). A New Formulation of Zipf’s Meaning-Frequency Law…
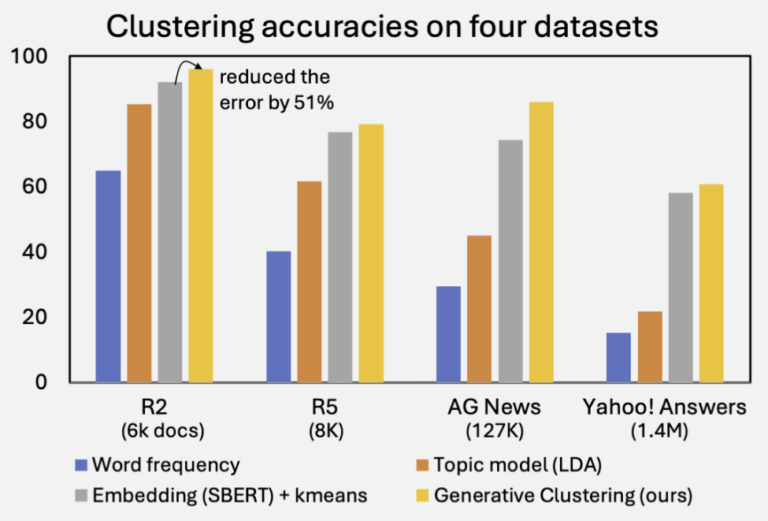
クラスタリングは、機械学習やデータマイニングにおける基本的な技術であり、現実世界における自己組織化パターンを理解するための強力な手段です。 その本質は情報理論的であり、ドキュメント集合に対して「いくつクラスタが存在し、各ドキュメントはどのクラスタに属するか」という最も単純な仮説を立て、それに基づいて情報の損失を最小化することにあります。 しかしこの10年間で、情報理論的な観点に基づかないクラスタリング手法が主流となってきました。ドキュメントを単語の出現確率分布として表す代わりに、BERTのような強力な言語モデルによって密なベクトルとして表現する手法が一般化したためです。これらの埋め込みベースの手法は効果的ですが、自然な確率的解釈が難しく、情報理論の視点は次第に薄れていきました。 本研究では、生成言語モデルを活用することで、この古典的な情報理論的アプローチを再興します。 特に、Doc2Queryモデルを用いて、各ドキュメントを「生成されるテキストの確率分布」として表現します。この生成空間は離散かつ無限ですが、正則化付き重要サンプリング(Regularized Importance Sampling) により、その分布とKLダイバージェンスを高精度に推定します。 つまり、私たちの手法はクラスタリングと統計推定を一体として行います。実験では、4つの標準的なクラスタリングデータセットにおいて、従来の埋め込みベースの強力な手法を大きく上回る性能を達成しました。 参考文献
ニュース記事と株価履歴を用い、株式のベクトル表現(Stock Embedding)を機械学習により獲得します。このベクトル表現は、金融予測モデルにおいて、財の計算表現として用いることができるものですが、ほかにも数多くの応用が考えられます。たとえば、複数の株に投資する際、その比率を最適に決めるポートフォリオ最適化のために用いることができます。米国市場のデータを用いると、ニュース記事から得た株ベクトル表現を用いると、従来の株価データのみを使用する方法に比べて2.8倍の利益が得られます。ロンドン、東京、上海市場などでも、株ベクトル表現を用いたポートフォリオで、利益が増大することが実証されています。 参考文献
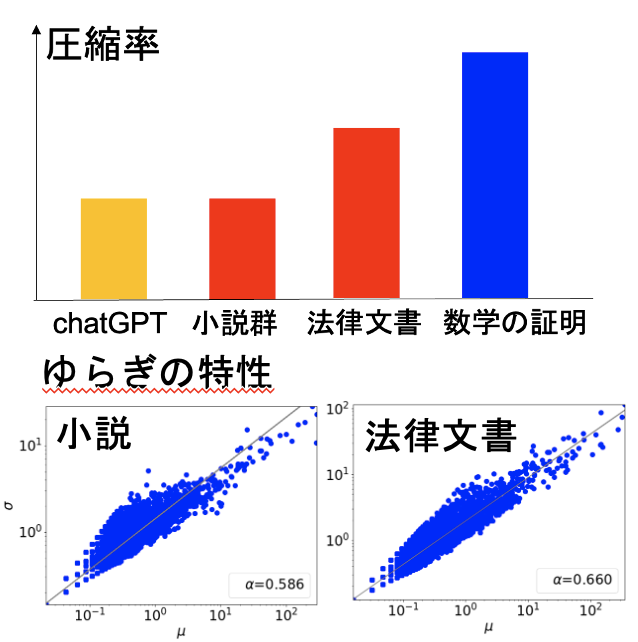
文書にはさまざまな観点から複雑さがあります。たとえば、圧縮率や、ゆらぎの度合いなどです。複雑さは、文書がどの程度「推論」に基づくものであるか、により異なります。たとえば、数学の証明のコーパスは、文学作品よりも、圧縮率は大きいです。法律文書のように、自然言語の文書の中でも、推論に基づく文書は、数学の証明に似た性質を持ちます。推論の度合いと複雑さの関係を調べ、法律文書やプログラムの工学に必要な言語モデルを考えています。
Strahler数はもともと川の分岐の複雑さを特徴付けるために提案され、計算木などに応用されてきました。この研究では、Strahler数を自然言語の文の木構造の複雑さを計測するために適用しました。自然言語の文のStrahler数の上限と下限が、3から4になることがわかりました。この数は、文を処理する際に必要なメモリ領域の数を示し、文の長さに応じて対数的に増加するものです。 参考文献
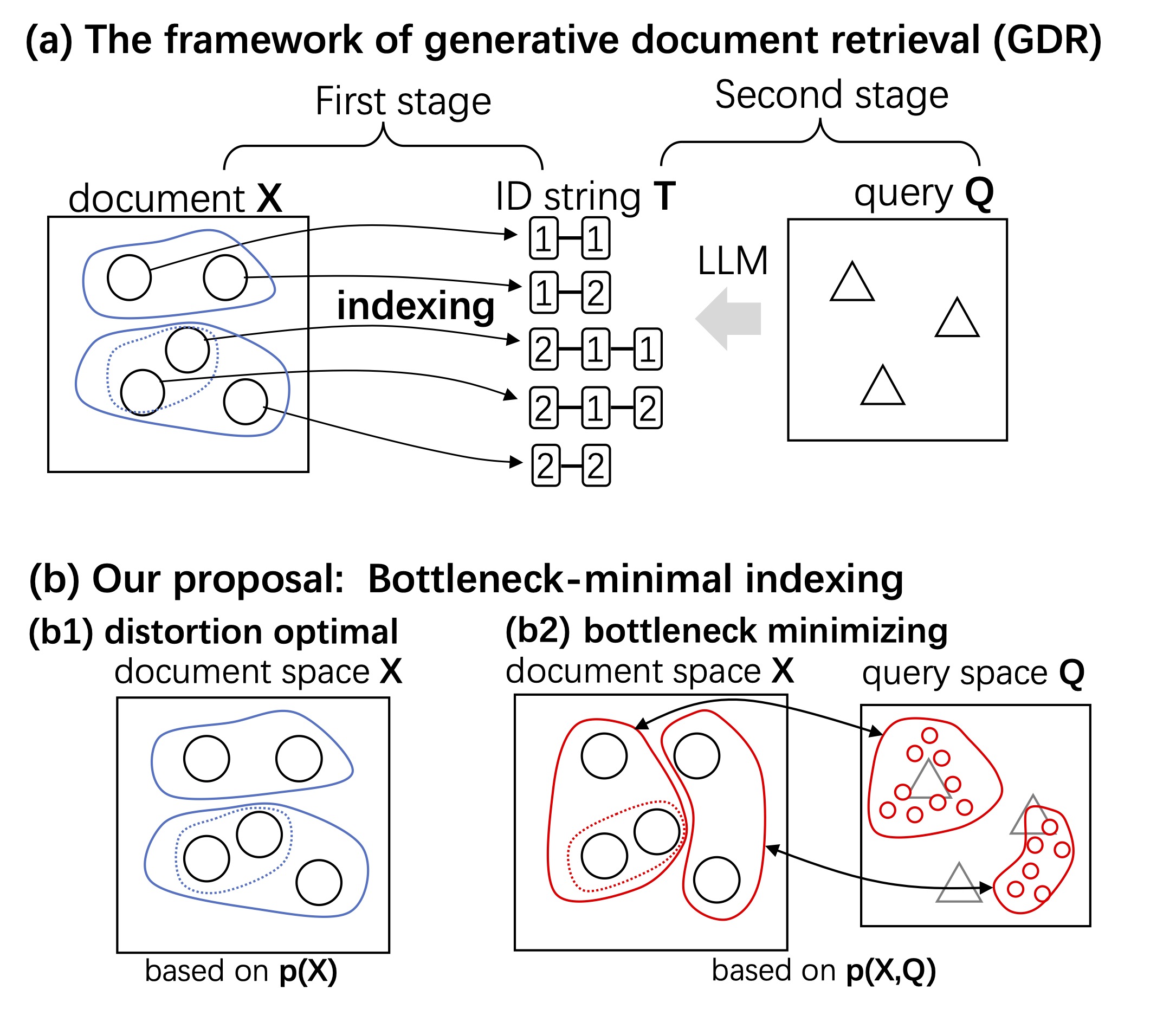
情報理論の視点から生成的文書検索(GDR)を再考し、新しい文書の索引を提案しています。文書をx∈X 、索引をt∈T 、検索クエリq∈Qとする時、GDRでは Q を T にマッピングするようにニューラルネットワークを訓練します。GDRは、文書 X からクエリ Q へ、索引 T を介して、より多くのビットを伝送する系とみなすことができます。シャノンのレート歪み理論を適用することにより、GDRにおける情報伝達ボトルネックを小さくする索引 T を設計することができます。 参考文献
自然言語の相関次元は、大規模言語モデルによって生成された高次元ベクトル列にGrassberger-Procacciaアルゴリズムを適用することで測定されます。この方法は、以前はユークリッド空間でのみ研究されていましたが、本研究では、統計多様体上にFisher-Rao距離を用いて再定式化しました。相関次元は、普遍的に約6.5であることがわかりました。この値は単純な離散ランダム列のそれよりも小さく、Barabási-Albert過程のそれよりも大きいです。 参考文献
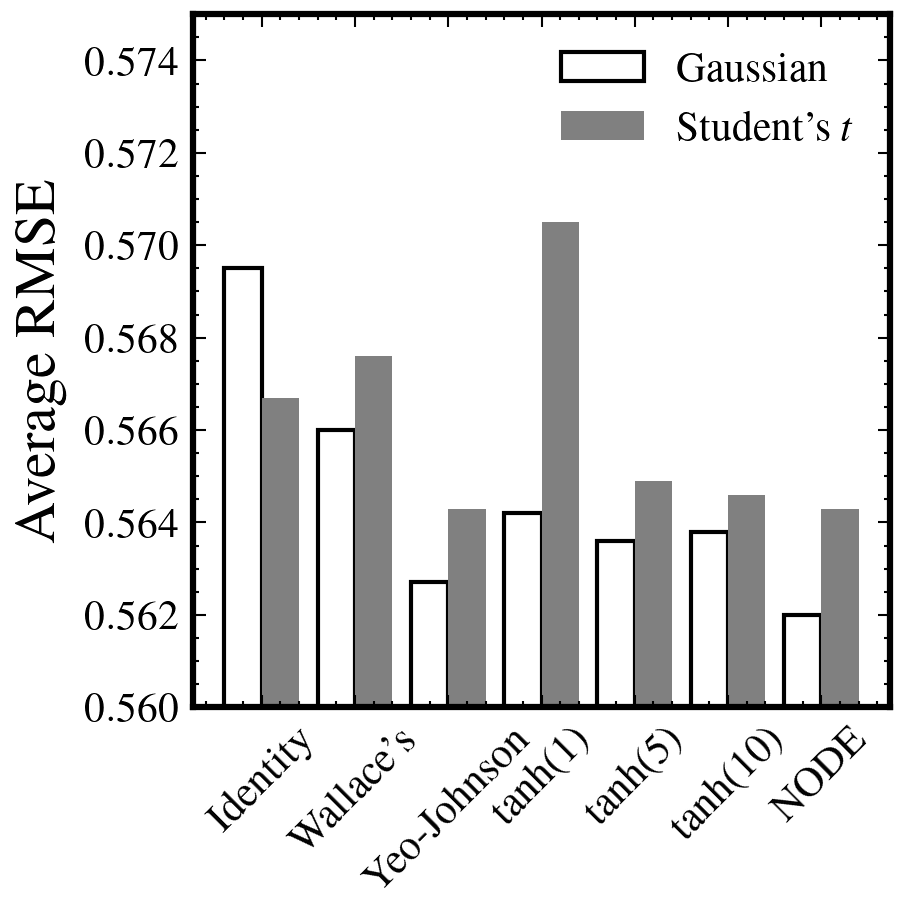
この研究では、実現ボラティリティ(RV)の予測のために、正規化フローを使用した新しい機械学習モデルが提案されています。RVの特性を考慮し、変換と予測モデルを共同でトレーニングする方法が提案され、最大尤度目的関数に基づくトレーニングが行われます。この新しいアプローチは、100銘柄のデータセットにおいて、従来の分析的またはニューラルネットワークに基づく変換方法よりも優れた結果を示しています。 参考文献
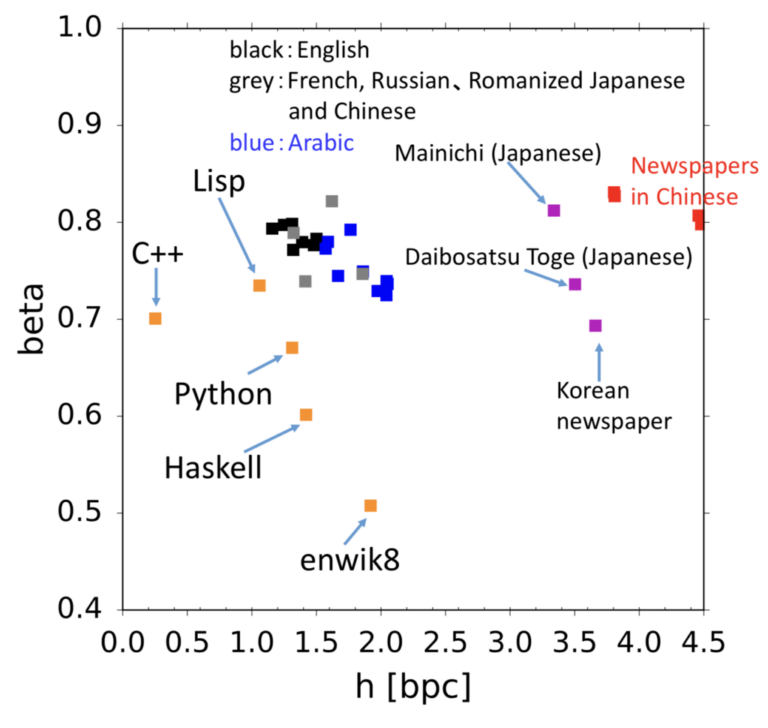
言語、音楽、プログラムなど記号に基づく時系列のエントロピーレートを算出し、 人の記号の時系列に内在する複雑さを探求しています。長さnの時系列の場合の数を、パラメータhを用いて2hnとして考えてみます。まずランダムなビット列の場合はh=1です。では英語を仮に27文字と考えたとしてその数は27n、にはなりません。なぜなら自然言語の場合、qの後にはuしか続かないなど言語的な制約がさまざまにあるからです。情報理論の父シャノンはh=1.3と算出していますが、hの推定は難しい問題で、自然言語のhが正なのかすら未だにわかっていません。研究室では自然言語に加え、音楽・プログラム・金融データなどさまざまな記号時系列の複雑さを推定する研究を行っています。 参考文献