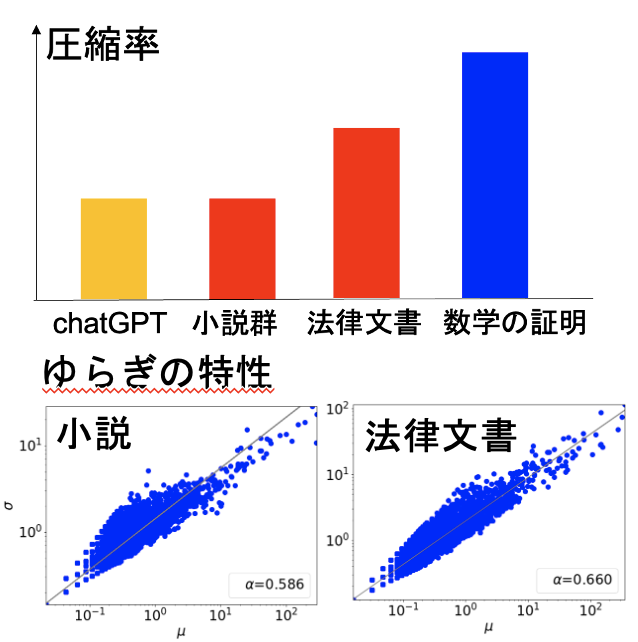
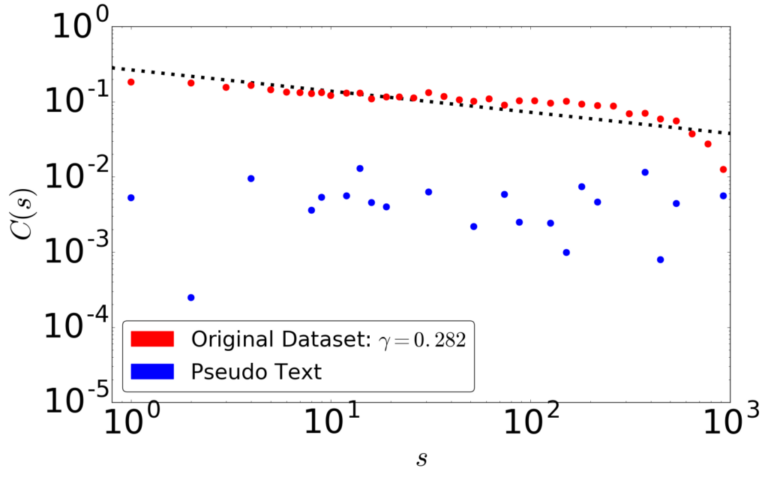
大規模言語モデル(LLM)は自然言語生成において顕著な進歩を遂げている一方で、パープレキシティが低い場合であっても、反復や文のちぐはぐさといった不可解な挙動を依然として示す。このことは、局所的な予測精度を重視するあまり長距離の構造的複雑さを見落としてしまうという、従来の評価指標の本質的な限界を浮き彫りにしている。本研究では、自己相似性を測るフラクタル幾何学的な尺度である「相関次元」を導入し、言語モデルの観点から知覚されるテキストの認識論的複雑さを定量化する。この指標は、言語の階層的な再帰構造を捉えることで、局所的および大域的な性質を統一的な枠組みのもとで橋渡しする役割を果たす。大規模な実験を通じて、相関次元が (1) 事前学習過程における3つの異なるフェーズを明らかにし、(2) 文脈依存的な複雑さを反映し、(3) モデルのハルシネーション傾向を示唆し、さらに (4) 生成テキストに現れる複数のデジェネレーション形態を高い信頼性で検出できることを示す。我々の手法は計算効率に優れ、4ビット精度までのモデル量子化に対しても頑健であり、Transformer や Mamba をはじめとする広範な自回帰アーキテクチャに適用可能である。また、LLM の生成ダイナミクスに対して新たな洞察を提供する。 参考文献 Du, X., & Tanaka-Ishii, K….
複雑系としての自然言語の数理と機械学習
自然言語を複雑系と捉え、言語データに内在する大域的性質ならびにその言語構造との関係を、フラクタルやカオスの視点から基礎的に研究しています。言語の数理構造をふまえ、言語の数理モデルを構築し、自然言語処理に応用しています。
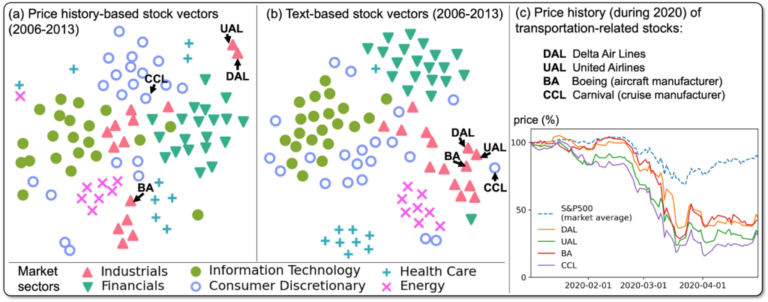
複雑系としての言語の大域的特性は、金融やコミュニケーションネットワークなど社会的複雑系に共通する性質でもあります。この共通性を生かし、社会的複雑系の大規模な解析や予測を、言語的な視点から行っています。

言語の複雑系科学・数理的性質
- 言語の非定常特性・長期記憶の計測
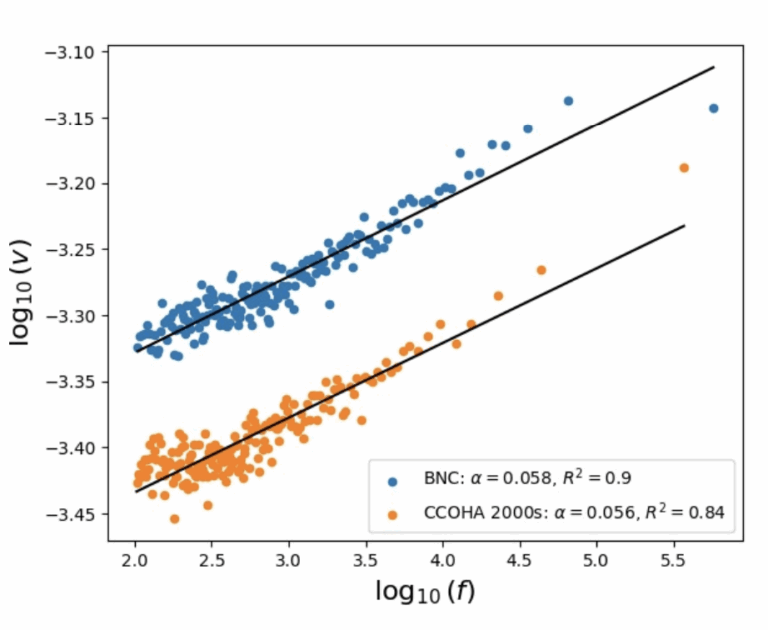
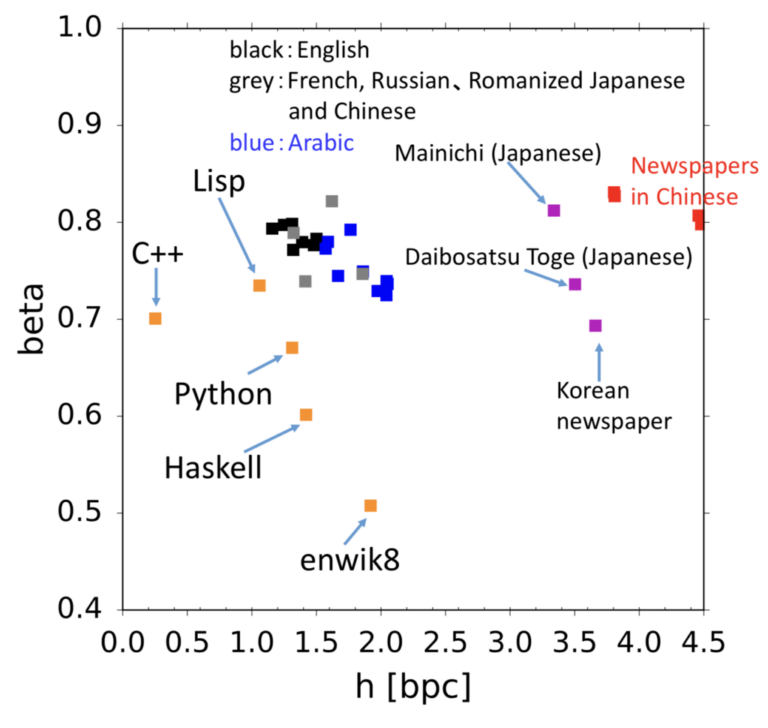
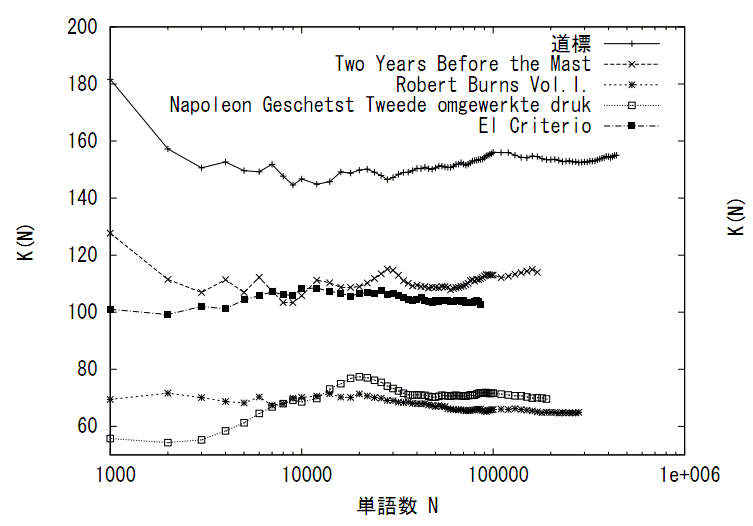
- 言語の系のスケーリング則
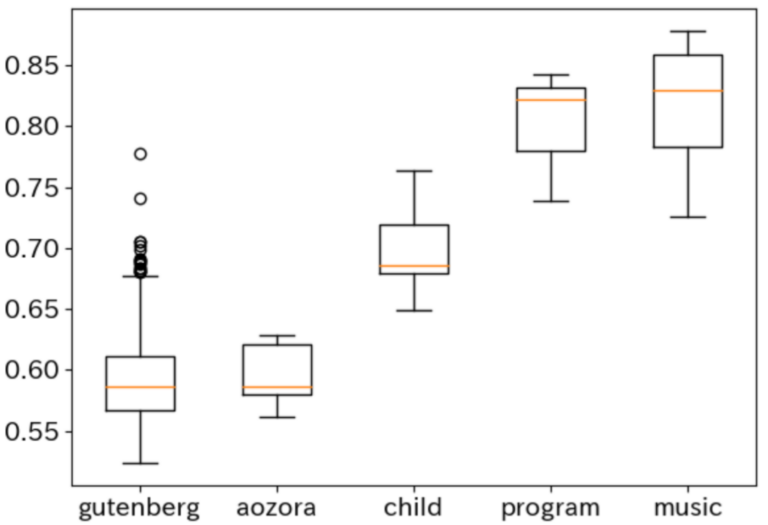
- 言語の複雑さの計測
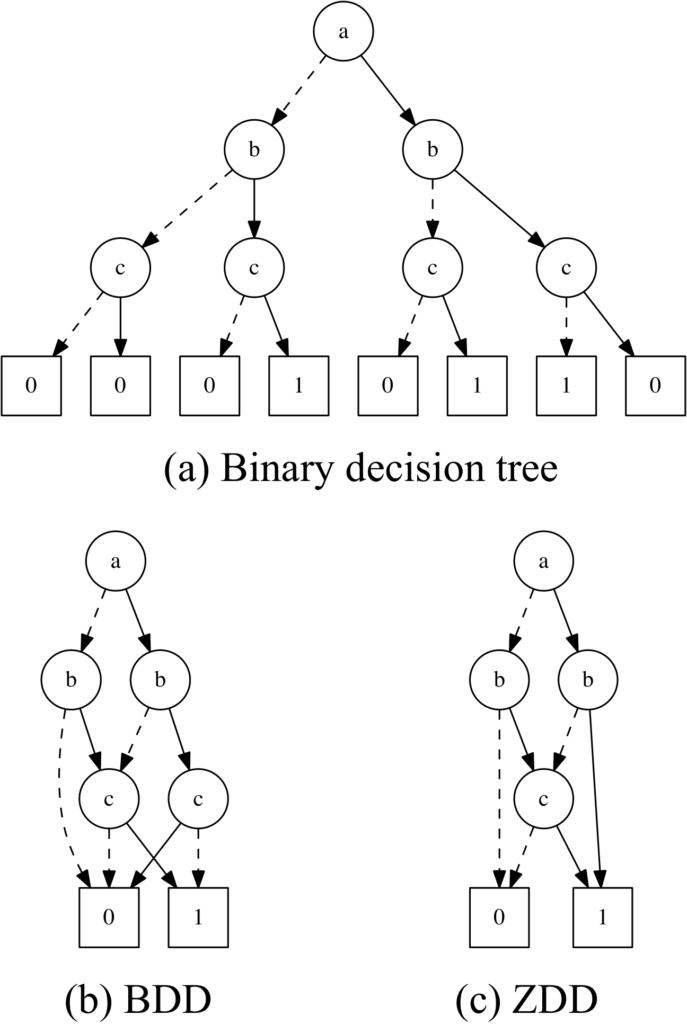
- 文書・文構造の数理
機械学習に基づく言語の数理モデル
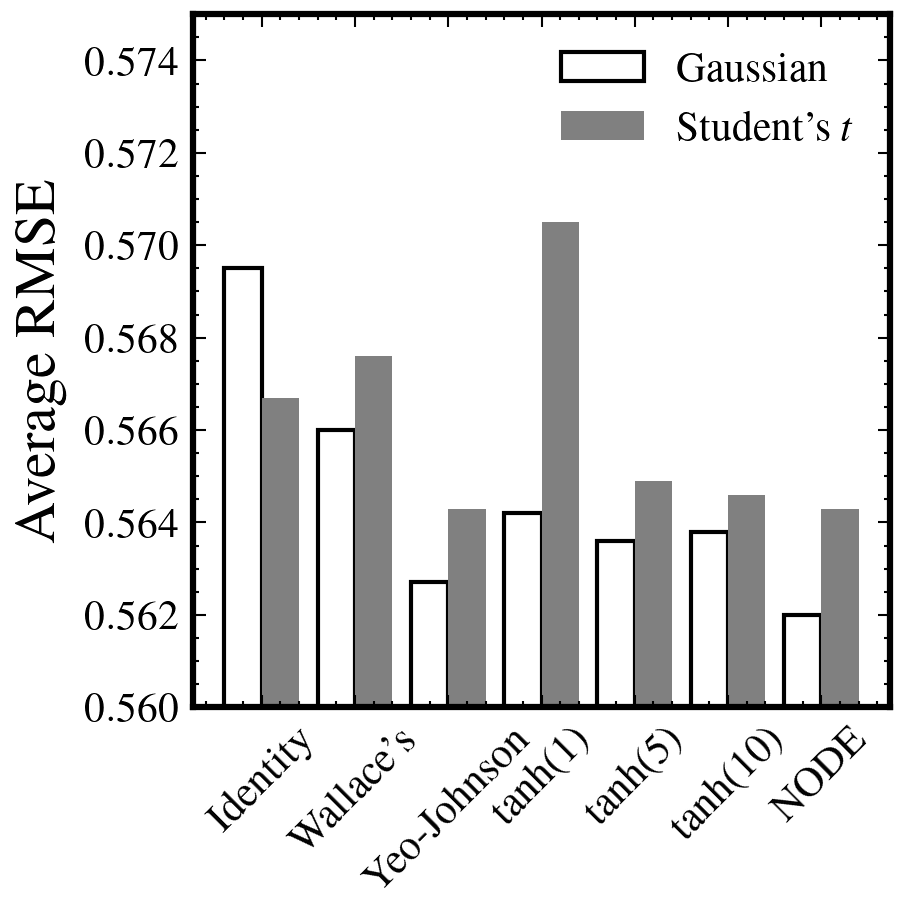
- 言語の統計的性質を再現する数理モデル
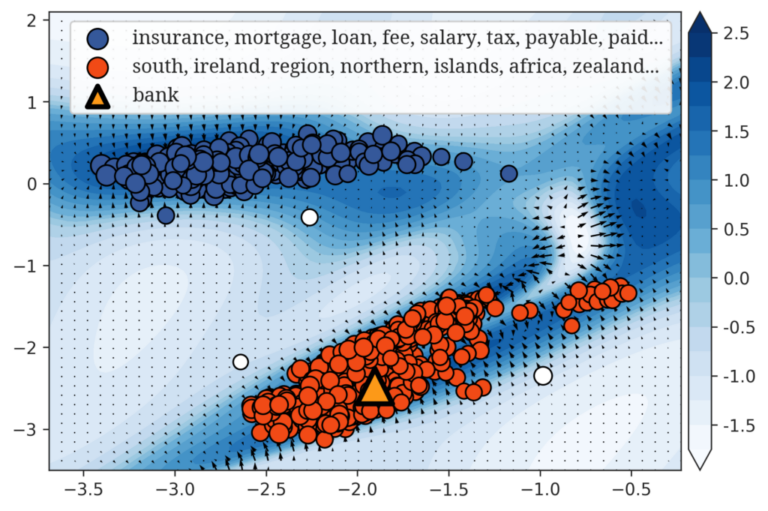
- 埋め込み表現手法
- 長期記憶と生成モデル
- 複雑系の性質を持つ系列の機械学習手法
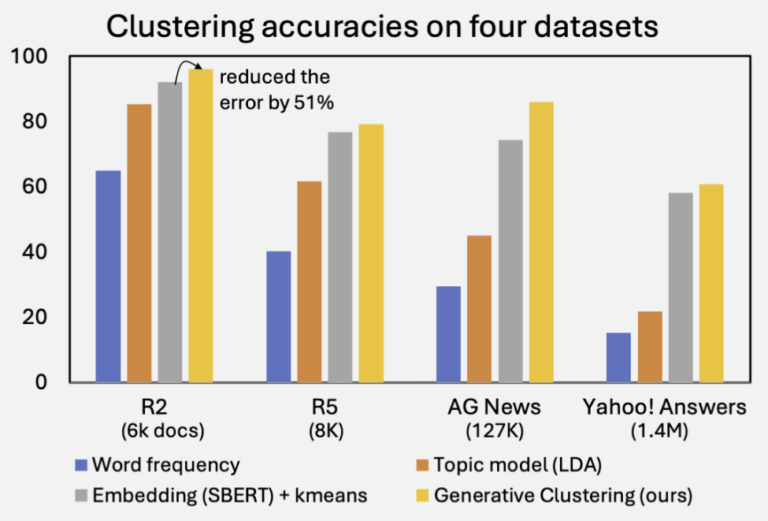
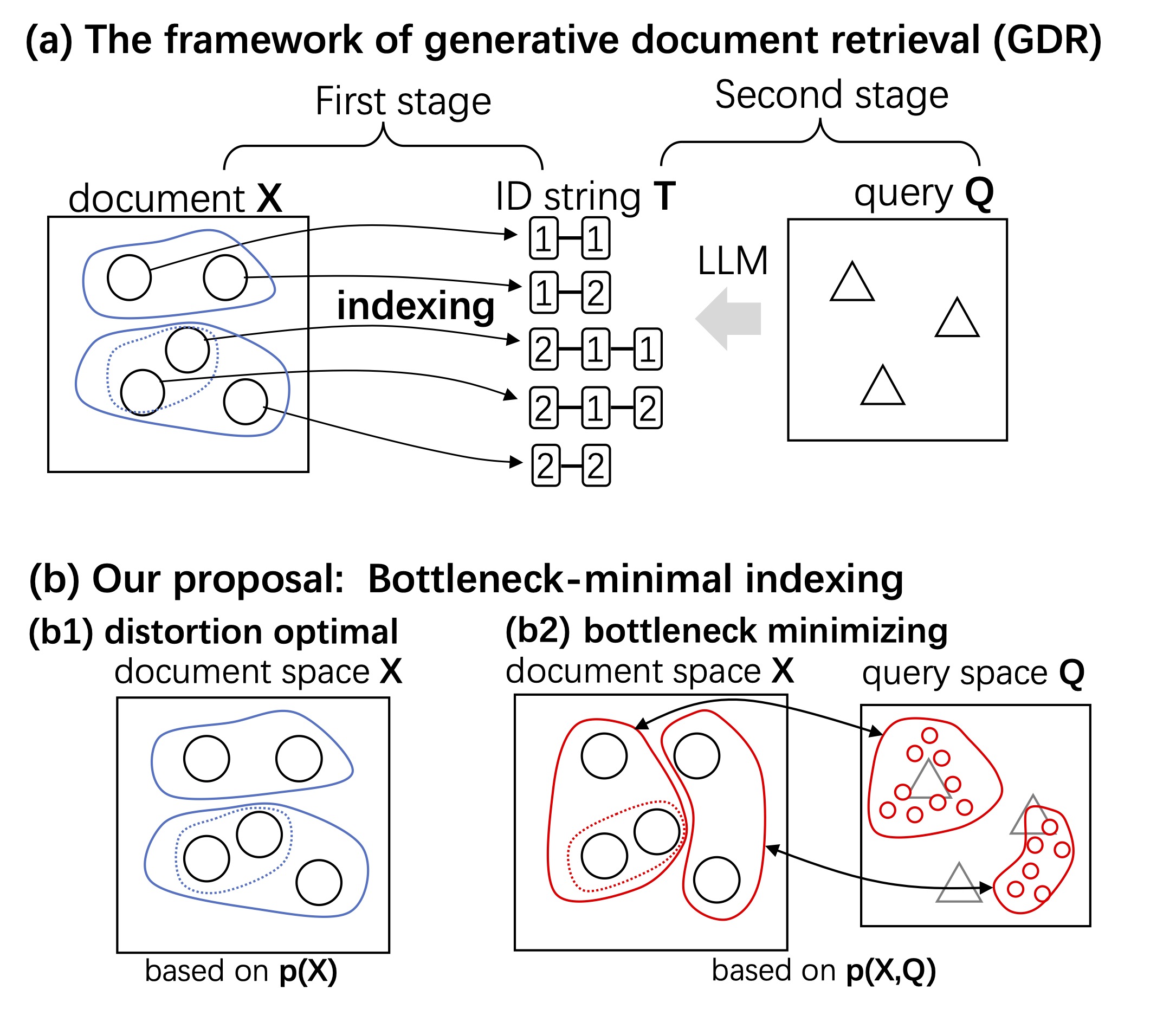
- 言語モデルと文書検索の融合
言語的視点からの社会的複雑系の工学
- 社会的対象の埋め込み表現獲得手法
- 法律の複雑系科学と機械学習応用
- 言語データに基づく金融データの深層学習
- 推論に基づく言語対象の工学